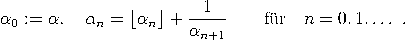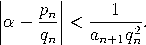3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.2. Kettenbrüche
_______________________________________________________________________________
|
|
Zunächst betrachten wir den euklidischen Algorithmus, welchen wir (gemäß der Notation aus III.1.) umschreiben als (1) für n ≤ m; dabei steht ⌊x⌋ für die größte ganze Zahl ≤ x (auch Gaußklammer bzw. Ganfteil genannt). Setzen wir an = ⌊rn−1/rn⌋, so ergibt sich
Der typographische Albtraum 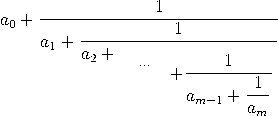 heißt Kettenbruch (engl. continued fraction); die an nennt man Teilnenner. Wir notieren einen solchen Kettenbruch kurz mit ![[a ,a ,a ] = a2a1a0 +-a2-+-a0-. 0 1 2 a2a1 + 1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch5x.gif)
und ![[a0,a1,...,an] = a0 + ----1------= [a0,[a1,...,an]]. [a1,...,an ]](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch7x.gif) Für n ≤ m nennen wir [a0,a1,…,an] den n-ten Näherungsbruch an [a0,a1,…,am]. Wir definieren desweiteren 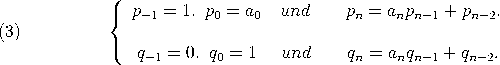 Die Berechnung der Näherungsbrüche erfolgt leicht mit Hilfe von |
Satz. Für 0 ≤ n ≤ m gilt
![pn-= [a0,a1,...,an]. qn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch9x.gif)
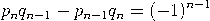
|
Beweis per Induktion nach n. Der Fall n = 0 ist trivial. Der Fall n = 1 folgt unmittelbar aus ![a1a0 + 1 p1 [a0,a1] = ---------= --. a1 q1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch11x.gif) ![[ ] --1-- [a0, a1,...,an,an+1] = a0,a1,...,an + an+1 .](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch12x.gif) 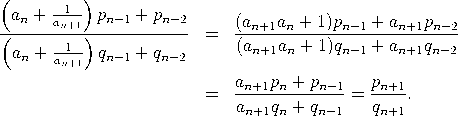 was die Induktion und den Beweis der ersten Aussage abschließt. Mittels (3) ist 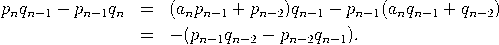 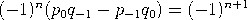 |
Jetzt weisen wir den Teilnennern an und somit auch dem Kettenbruch [a0,a1,…,am] numerische Werte zu. Wir fordern a0∈ℤ und an∈ℕ für 1 ≤ n < m, sowie am≥ 1. Sei jetzt α irgendeine rationale Zahl. Dann gibt es teilerfremde ganze Zahlen a und b > 0, so dass α = ab. Es folgt aus der Variation des euklidischen Algorithmus (1) angewandt auf r−1 = a und r0 = b, dass α als endlicher Kettenbruch dargestellt werden kann: ![[ ] a-= [a0,a1,a2,...,am ] , wobei an = rn−1-. b rn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch16x.gif) ![[a0,a1,a2,...,am ] = [a0,a1,a2, ...,am − 1,1];](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch17x.gif) Jetzt wollen wir Kettenbrüche zu nicht notwendig rationalen Zahlen bilden. Wir können den Algorithmus (1) zur Berechnung der Kettenbruchentwicklung von rationalen Zahlen umschreiben als
Setzen wir an = ⌊αn⌋, so erhalten wir α = [a0,a1,…,an,αn+1]. Dieser Algorithmus ist der Kettenbruchalgorithmus. Ist α rational, dann bricht die Iteration nach endlich vielen Schritten ab und der Kettenbruchalgorithmus ist nichts anderes als der euklidische Algorithmus in Verkleidung. Beispiel. ![[a ,a ,...] := lim [a ,a ,...,α ]. 0 1 m→ ∞ 0 1 m](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch19x.gif) |
|
Satz. Sei α = [a0,a1,…,an,αn+1] irrational mit Näherungsbrüchen pn/qn. Dann gilt 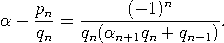
und ![pn α = lim ---= [a0,a1,a2,...]. n→∞ qn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch22x.gif) |
|
Beweis. Zunächst bemerken wir, dass alle unsere Beobachtungen über endliche Kettenbrüche sich auf unendliche Kettenbrüche übertragen - insbesondere (3) und der vorherige Satz. Eine kurze Berechnung zeigt 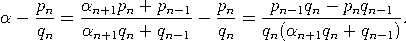 Der vorherige Satz impliziert damit die erste Behauptung. Wegen an+1≤ αn+1 folgt ferner 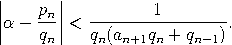 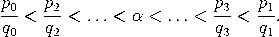 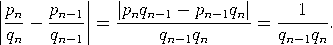 |
Sehr interessant sind auch so genannte periodische Kettenbrüche. |

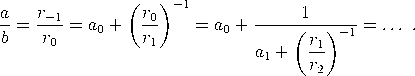
![[ ] [a ,a ,...,a ] = a ,a ,...,a + -1- 0 1 n 0 1 n−1 an](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch6x.gif)