3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.3. Gesetz der besten Approximation
|
|
Gegeben zwei reelle Zahlen α = [a0,…,an,αn+1] und α' = [a0,…,an,αn+1'] mit denselben ersten Teilnennern, dann folgt, dass jedes α'', das zwischen α und α' liegt, eine Kettenbruchentwicklung besitzt, die mit denselben Teilnennern startet, wie die von α und α', nämlich: ![α'' = [a ,...,a ,α '' ] 0 n n+1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste0x.gif) Der zweite Satz aus dem vorherigen Kapitel zeigt, wie wichtig Kettenbrüche in der Theorie der diophantischen Approximation sind. Es folgt nämlich unmittelbar: Ist α = [a0,a1,…] irrational mit Näherungsbrüchen pn/qn, dann gilt 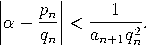 Diese Beobachtung ist kein Wunder wie Lagrange 1770 bewiesen hat: |
|
Satz (Gesetz der besten Approximation). Sei α irgendeine reelle Zahl mit Näherungsbrüchen pn/qn. Ist n ≥ 2 und sind p,q natürliche Zahlen mit 0 < q ≤ qn und p/q ≠ pn/qn, so gilt  |
| Das Gesetz der besten Approximation besagt also, dass die besten rationalen Approximationen durch die Näherungsbrüche der Kettenbruchentwicklung gegeben sind. Dies lässt sich an Beispielen veranschaulichen - ein besonders Prominentes ist unser täglich verwendetes Papierformat Din-A. |
|
Beweis. Wir dürfen annehmen, dass p und q teilerfremd sind. Wegen 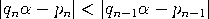 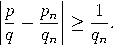 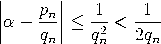 , ,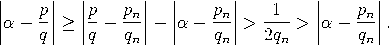 Es verbleibt der Fall: qn−1< q < qn. Das lineare Gleichungssystem 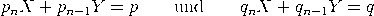 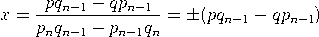 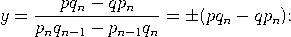 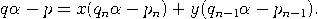 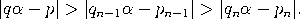 |
|
Eine Irrationalzahl α heißt quadratisch irrational, falls sie Wurzel eines quadratischen Polynoms mit ganzzahligen Koeffizienten ist; da α irrational ist, ist das Polynom irreduzibel (d.h. nicht als Produkt zweier linearer Polynome mit rationalen Koeffizienten darstellbar). Jede relle quadratische Irrationalität lässt sich also darstellen als
wobei a,b ∈ ℤ, c,d ∈ ℕ. Dies ergibt sich unmittelbar durch das Lösen der zu Grunde liegenden quadratischen Gleichung. Alle Beispiele dieser quadratischen Irrationalitäten haben folgendes gemein: Ihre Kettenbruchentwicklung ist periodisch! Hierbei heißt ein Kettenbruch [a0,a1,…] periodisch, falls es einen Index ℓ gibt, so dass an+ℓ = an für alle hinreichend großen n. Wir schreiben ![-------------- [a0,a1, ...,ar,ar+1,...,ar+ℓ] = [a0,a1,...,ar,ar+1,...,ar+ ℓ,ar+1,...,ar+ ℓ,...];](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste13x.gif)
wobei a1,a2,…,a2,a1 ein Palindrom ist. Dies wurde von Galois bewiesen, der tragisch in einem Duell verstarb und trotz seines jungen Alters unsterblich für die Algebra und Zahlentheorie ist. Wir verzichten hier auf den Beweis. |

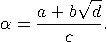
![[[ ] ------------------[---]] √ -- √ -- √ -- d = d ,a1,a2,...,a2,a1,2 d ,](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste14x.gif)