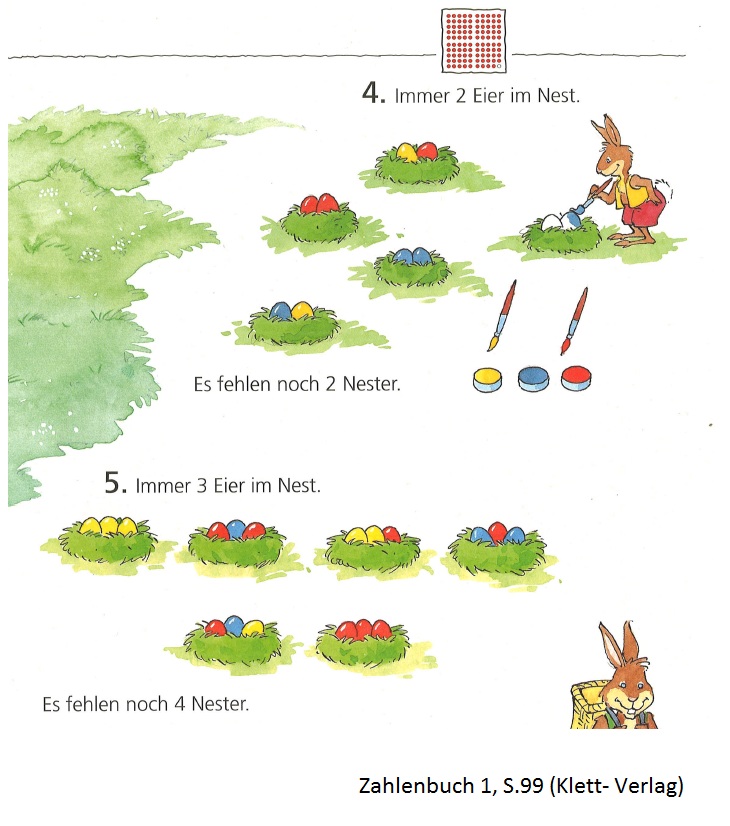
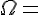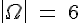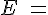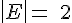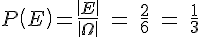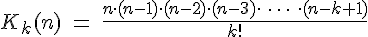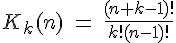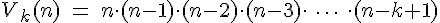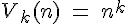- Welche Möglichkeiten gibt es, bestimmte Elemente einer endlichen Grundmenge unter bestimmten Voraussetzungen anzuordnen.
- Wie viele Möglichkeiten gibt es, bestimmte Elemente einer endlichen Grundmenge unter bestimmten Voraussetzungen anzuordnen.
Demokurs: Grundlagen der Mathematik für die Grundschule (Geometrie und Stochastik)
Требуемые условия завершения
Demokurs
Grundlagen der Mathematik für die Grundschule
Grundlagen der Mathematik für die Grundschule


Grundlagen der Mathematik für die Grundschule
(Arithmetik – Geometrie – Sachbezogene Mathematik)
(Arithmetik – Geometrie – Sachbezogene Mathematik)

Im Kapitel Kombinatorik finden Sie:
- Grundaufgaben der Kombinatorik (Permutation, Variation, Kombination)
- Einsendeaufgaben zum Thema Kombinatorik.

Bedeutung für die Grundschule
Neben der Wahrscheinlichkeitsrechnung und der Statistik ist die Kombinatorik ein weiterer Bestandteil der Stochastik. Die Kombinatorik ist bezüglich der Bildungsstandards dem Punkt „Daten, Häufigkeit und Wahrscheinlichkeit“ der inhaltsbezogenen Standards zuzuordnen (vgl. ISB/ BILDUNGSSTANDARDS, S.11).
Im bayerischen Lehrplan ist die Kombinatorik dem Bereich der sachbezogenen Mathematik zuzuordnen. So sollen beispielweise in der 2.Jahrgangsstufe bei der Arbeit an Sachsituationen Aufgaben zur Kombinatorik behandelt werden (vgl. ISB/ LEHRPLAN, S.101). Diese Aufgaben eignen sich zur inneren Differenzierung, da Leistungsschwächere einige Möglichkeiten durch Probieren finden können und Leistungsstärkere alle Möglichkeiten erforschen können. Aber trotzdem arbeiten alle Schüler an der gleichen Aufgabe. Grundsätzlich sollen Schülerinnen und Schüler Sachaufgaben mit kombinatorischem Inhalt nachvollziehen, verbalisieren und gegebenenfalls Skizzen zur Lösung anfertigen können. Dabei sind zwei Aufgabenstellungen zu unterscheiden, die in der Grundschule Relevanz besitzen:
Dieses Kapitel soll Ihnen die Gelegenheit bieten, die Grundaufgaben der Kombinatorik kennenzulernen. Im Mathematikunterricht der Grundschule sollen Sie diese Vielfalt an möglichen Aufgaben didaktisch reduziert umsetzen können und zwar mit der Zielsetzung sich nicht nur auf eine der Grundaufgaben (Permutation, Variation und Kombination) zu beschränken. Neben dem Erstellen abwechslungsreicher Aufgaben ist die Behandlung unterschiedlicher und vielfältiger Bearbeitungsmöglichkeiten (Probieren, Produktregel, Baumdiagramm, Skizzen) kombinatorischer Aufgaben das Ziel dieses Kapitels. Nicht alle Möglichkeiten sind grundschulrelevant, aber als kommende Lehrkraft sollten sie trotzdem auch komplexere kombinatorische Aufgaben lösen können.

Grundlegende Begriffe
Im vorherigen Kapitel wurde die klassische bzw. die Laplace- Wahrscheinlichkeit folgendermaßen hergeleitet:
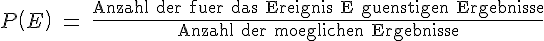
Das Berechnen der Wahrscheinlichkeiten bei Laplace-Experimenten beinhaltet das Zählen von Ergebnissen. Bei vielen Laplace-Experimenten sind die Anzahl der für das Ereignis E günstigen Ergebnisse und die Anzahl der möglichen Ergebnisse relativ leicht zu bestimmen.
Im vorherigen Kapitel wurde die klassische bzw. die Laplace- Wahrscheinlichkeit folgendermaßen hergeleitet:
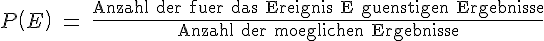
Das Berechnen der Wahrscheinlichkeiten bei Laplace-Experimenten beinhaltet das Zählen von Ergebnissen. Bei vielen Laplace-Experimenten sind die Anzahl der für das Ereignis E günstigen Ergebnisse und die Anzahl der möglichen Ergebnisse relativ leicht zu bestimmen.
Beispiel:
Zufallsgerät: Urne mit zwei gelben, einer roten und drei blauen Kugeln
Zufallsexperiment: Ziehen einer Kugel aus der Urne
Zufallsgerät: Urne mit zwei gelben, einer roten und drei blauen Kugeln
Zufallsexperiment: Ziehen einer Kugel aus der Urne

Das Abzählen der Möglichkeiten gelingt aber nicht immer so einfach wie im obigen Beispiel. So könnte man auch nach den Möglichkeiten fragen, 2 Kugeln in einer bestimmten Reihenfolge zu ziehen. Es gibt verschiedene Möglichkeiten den Schwierigkeitsgrad für die Abzählprozesse zu erhöhen:
- Werden alle möglichen Elemente verwendet?
- Ist die Reihenfolge der Anordnung wichtig?
- Sind Wiederholungen zugelassen? (z.B. Zurücklegen einer Kugel)
Die Kombinatorik dient als Hilfsmittel, das Abzählen der Ergebnisse auch bei schwierigeren Laplace- Experimenten zu erleichtern. Dabei lassen sich 3 Grundaufgaben unterscheiden:
- Kombinationen
- Variationen
- Permutationen als Sonderfall der Variationen

Definition Produktregel (Grundregel des Zählens):
Wenn eine Folge von Entscheidungen zu treffen ist, bei der es für die erste Entscheidung p Möglichkeiten, für die zweite Entscheidung q Möglichkeiten, für die dritte Entscheidung r Möglichkeiten gibt, usw. dann gibt es für die Folge aller Entscheidungen p q
q  r
r 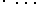 Möglichkeiten. (vgl. PANKNIN, 1972, S.33ff.)
Möglichkeiten. (vgl. PANKNIN, 1972, S.33ff.)
Wenn eine Folge von Entscheidungen zu treffen ist, bei der es für die erste Entscheidung p Möglichkeiten, für die zweite Entscheidung q Möglichkeiten, für die dritte Entscheidung r Möglichkeiten gibt, usw. dann gibt es für die Folge aller Entscheidungen p
 q
q  r
r 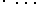 Möglichkeiten. (vgl. PANKNIN, 1972, S.33ff.)
Möglichkeiten. (vgl. PANKNIN, 1972, S.33ff.) 
Kombination

Definition Kombination:
Jede Anordnung, die nicht alle Elemente einer vorgegebenen Menge gleichzeitig verwendet und auf die Beachtung der Reihenfolge verzichtet, nennt man Kombination. (vgl. PANKNIN, 1972, S.40ff.)
Jede Anordnung, die nicht alle Elemente einer vorgegebenen Menge gleichzeitig verwendet und auf die Beachtung der Reihenfolge verzichtet, nennt man Kombination. (vgl. PANKNIN, 1972, S.40ff.)
Zusatz:
Ohne Beweis sei auch hier darauf hingewiesen, dass mithilfe der Produktregel die Anzahl K der Kombinationen von k Elementen bei einer vorgegebenen Menge von n Elementen mit folgenden Formeln berechnet werden kann:
Ohne Beweis sei auch hier darauf hingewiesen, dass mithilfe der Produktregel die Anzahl K der Kombinationen von k Elementen bei einer vorgegebenen Menge von n Elementen mit folgenden Formeln berechnet werden kann:
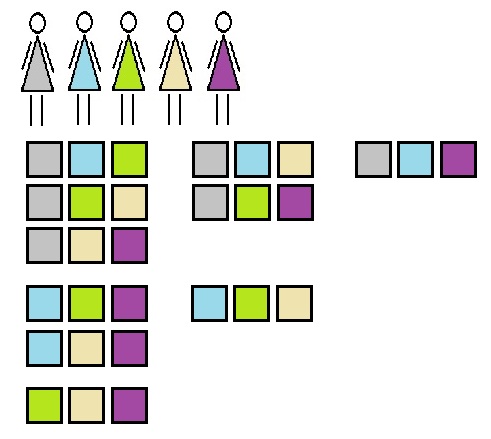
Beispiel: Bei einer Casting- Show werden für eine Sonderprüfung aus 5 Teilnehmerinnen 3 ausgewählt. Wie viele mögliche Dreiergruppen gibt es?
- Probieren: Diese Strategie kann bei Mengen mit einer geringen Anzahl von Elementen gelingen. An dieser Stelle könnte man die Szene mit 5 Schülerinnen oder Schülern nachspielen und die Lösungen ikonisch festhalten.
- Produktregel/ Formel:
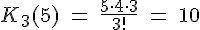
- Strategisches Vorgehen: Diese Strategie funktioniert nur mit geringen Elementanzahlen.
Vergleich der beiden Möglichkeiten der Kombination anhand von Beispielen:
Kombination ohne Wiederholung
Aus einer Urne mit 3 unterscheidbaren Kugeln sollen alle Kombinationen mit 2 Kugeln angegeben werden, die durch Ziehen ohne Zurücklegen vorkommen können.
→ (K1,K2), (K1,K3), (K2,K3)
Aus einer Urne mit 3 unterscheidbaren Kugeln sollen alle Kombinationen mit 2 Kugeln angegeben werden, die durch Ziehen ohne Zurücklegen vorkommen können.
→ (K1,K2), (K1,K3), (K2,K3)
Kombination mit Wiederholung
Aus einer Urne mit 3 unterscheidbaren Kugeln sollen alle Kombinationen mit 2 Kugeln angegeben werden, die durch Ziehen mit Zurücklegen vorkommen können.
→ (K1,K2), (K1,K3), (K2,K3), (K1,K1), (K2,K2), (K3,K3)
Aus einer Urne mit 3 unterscheidbaren Kugeln sollen alle Kombinationen mit 2 Kugeln angegeben werden, die durch Ziehen mit Zurücklegen vorkommen können.
→ (K1,K2), (K1,K3), (K2,K3), (K1,K1), (K2,K2), (K3,K3)

Variation

Definition Variation:
Jede Anordnung, welche nicht alle Elemente einer vorgegebenen Menge gleichzeitig verwendet und welche die Reihenfolge der Elemente beachtet, nennt man Variation. (vgl. PANKNIN, 1972, S.44ff.)
Jede Anordnung, welche nicht alle Elemente einer vorgegebenen Menge gleichzeitig verwendet und welche die Reihenfolge der Elemente beachtet, nennt man Variation. (vgl. PANKNIN, 1972, S.44ff.)

Zusatz:
Ohne Beweis darf hingenommen werden, dass sich die Anzahl der Variationen von k Elementen, welche aus der Grundmenge mit n Elementen entstammen, sich wie folgt berechnen lässt:
Ohne Beweis darf hingenommen werden, dass sich die Anzahl der Variationen von k Elementen, welche aus der Grundmenge mit n Elementen entstammen, sich wie folgt berechnen lässt:
Beispiel: Wie viele zweistellige Zahlen lassen sich aus den Ziffern 1,...,4 bilden? (Variation mit Wiederholung)
- Probieren: Führt schon fast an dieser Stelle zu weit. Diese Strategie versagt sehr schnell bei größeren Mengen.
- Formel:
Für die Zehnerstelle habe ich 4 Möglichkeiten. Für die Einerstelle habe ich ebenso 4 Möglichkeiten.
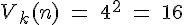
- Baumdiagramm oder weitere Schemata: Man stößt auch hier sehr schnell an die Grenzen der Umsetzung. Oft greift man daher auf verkürzte Baumdiagramme oder schemenhafte Darstellungen zurück.
Vergleich der beiden Möglichkeiten der Variation anhand von Beispielen:
Variation mit Wiederholung
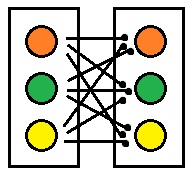
Aus einer Urne mit 3 farbigen Kugeln werden mit Zurücklegen 2 Kugeln nacheinander unter Berücksichtigung der Reihenfolge gezogen. Wie viele Variationsmöglichkeiten gibt es?

Es gibt 9 Variationsmöglichkeiten.
Variation ohne Wiederholung
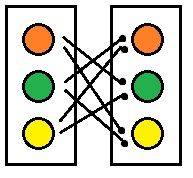
Aus einer Urne mit 3 farbigen Kugeln werden ohne Zurücklegen 2 Kugeln nacheinander unter Berücksichtigung der Reihenfolge gezogen. Wie viele Variationsmöglichkeiten gibt es?

Es gibt 6 Variationsmöglichkeiten.
Bei beiden Variationsmöglichkeiten werden nicht alle Elemente einer vorgegebenen Menge verwendet. Einen Sonderfall der Variation erhält man, wenn man alle Elemente verwendet, die Reihenfolge beachtet und ohne Wiederholung vorgeht. In diesem Fall entspricht k = n. Diese Grundaufgabe nennt man Permutation.

Permutation

Definition Permutation (permutare [lat.], vertauschen):
Jede Anordnung, die alle Elemente einer vorgegebenen Menge in einer bestimmten Reihenfolge enthält, nennt man Permutation. (vgl. PANKNIN, 1972, S.36ff.)
Jede Anordnung, die alle Elemente einer vorgegebenen Menge in einer bestimmten Reihenfolge enthält, nennt man Permutation. (vgl. PANKNIN, 1972, S.36ff.)
Zusatz:
Betrachtet man die Formel der Berechnung der Variationsmöglichkeiten ohne Wiederholung und setzt k = n, dann erhält man folgende Formel zur Berechnung der Anzahl der Permutationen:
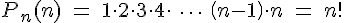
Betrachtet man die Formel der Berechnung der Variationsmöglichkeiten ohne Wiederholung und setzt k = n, dann erhält man folgende Formel zur Berechnung der Anzahl der Permutationen:
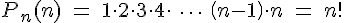
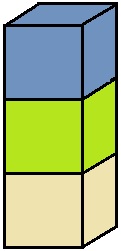
Beispiel: Sie wollen aus 3 verschiedenfarbigen Steinen Türme bauen, indem Sie die drei Steine aufeinandersetzen. Wie viele verschiedene Möglichkeiten gibt es?
- Probieren: Diese Strategie kann bei Mengen mit einer geringen Anzahl von Elementen gelingen. Hier würde es sich anbieten, die Türme selbstständig zu bauen.
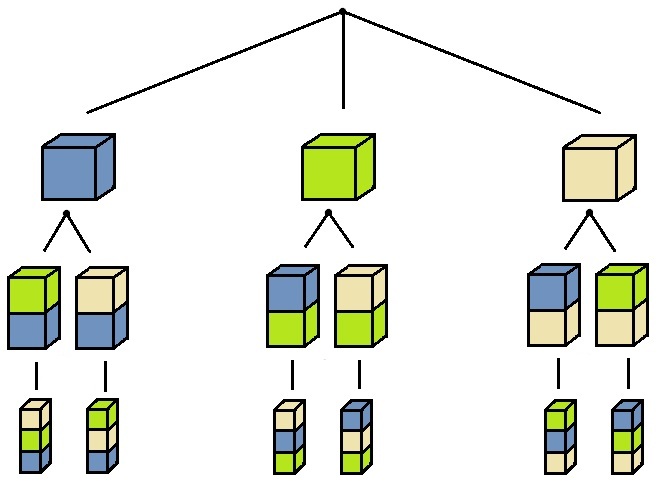
- Produktregel:
Nach der Produktregel gibt es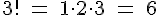 Möglichkeiten einen Turm aus den gegebenen verschiedenfarbigen Steinen zu bauen.
Möglichkeiten einen Turm aus den gegebenen verschiedenfarbigen Steinen zu bauen.
- Baumdiagramm: Diese Strategie wird ebenso wie das Probieren mit zunehmender Anzahl der Elemente schwieriger.

Schlüssel zur Bestimmung der Grundaufgabe der Kombinatorik
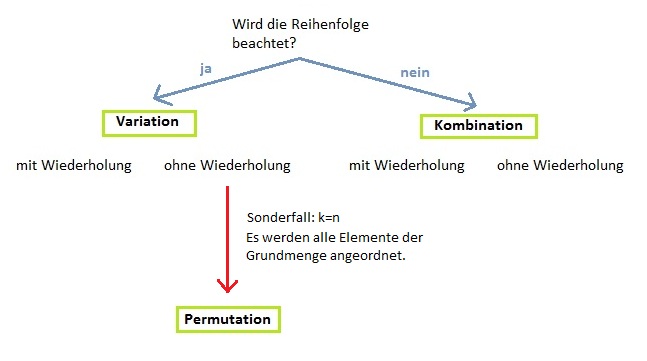


Kurz nachgedacht:
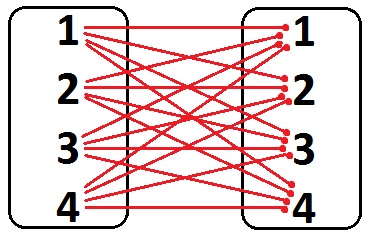
- Ordnen Sie in der nebenstehenden Zuordnungsaufgabe den gegebenen kombinatorischen Aufgaben die korrekte Grundaufgabe zu.
- Ermitteln Sie im nebenstehenden numerischen Test die gesuchte Anzahl der Möglichkeiten. Sie können dabei auf unterschiedliche Art und Weise vorgehen (Probieren, Skizze, Baumdiagramm, Produktregel).
- Sie haben die Buchstaben des Wortes „BAUM“ zur Verfügung.
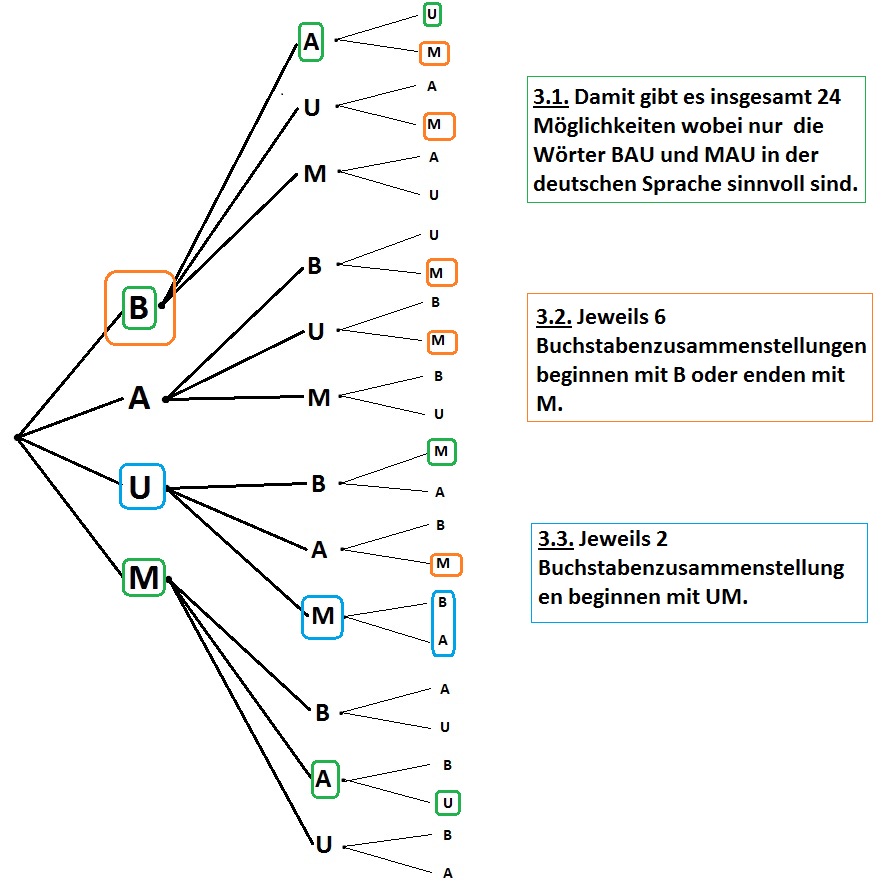
3.1. Wie viele Möglichkeiten gibt es, aus 3 Buchstaben des Wortes „BAUM“ ein Wort zu bilden und wie viele sind in der deutschen Sprache sinnvoll?
3.2. Wie viele der in 3.1. gefundenen Worte beginnen mit B und enden mit M?
3.3. Wie viele der Worte in 3.1. beginnen mit „UM“?
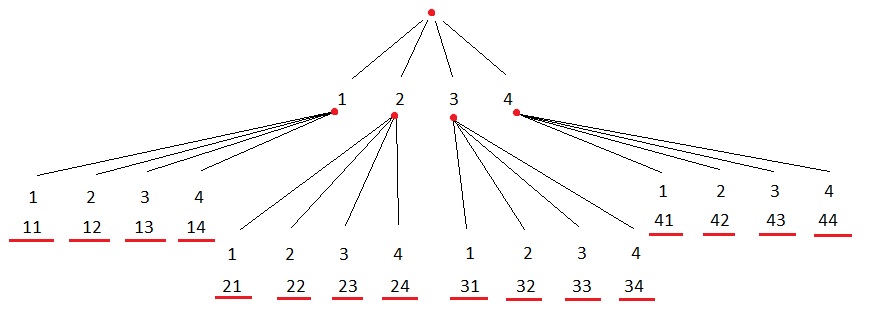
Lösungshinweis: Der einfachste Lösungsweg ist, dass man sich ein Baumdiagramm zeichnet und die entsprechenden Lösungen zusammenfasst und zählt.
Zeige/Verstecke Lösung
Zeige/Verstecke Lösung