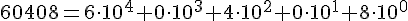- Das Prinzip der grundlegenden Bündelung:
Das Bündelungsprinzip besagt, dass die Elemente einer vorgegebenen Menge zu gleichmächtigen Teilmengen gruppiert werden. Die Mächtigkeit der Teilmengen wird durch die Wahl des Stellenwertsystems bestimmt. So werden im dezimalen Stellenwertsystem immer 10 Elemente und im Dualsystem (Binärsystem) immer 2 Elemente in einer Teilmenge zusammengefasst. Dabei gibt die Basis an, in welchen Teilmengen gebündelt werden soll. Teilmengen erster Ordnung müssen nach dem Bündelungsprinzip weiter zusammengefasst werden. Dieser Vorgang wird so lange weitergeführt, bis keine Bündel nächsthöherer Ordnung mehr gebildet werden können. Die Ziffern geben uns die Anzahl der Bündel an. - Das Stellenwertprinzip:
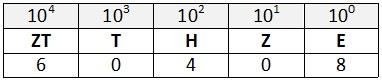
Notiert man das Ergebnis des oben beschriebenen Bündelungsprozesses, so erhält man eine bestimmte Ziffernfolge (Ziffern der niedrigsten Bündelungsstufe stehen rechts). Die Position der Ziffern übermittelt damit nicht nur die Anzahl der Bündel, sondern auch die Art des Bündels (Bündel n-ter Ordnung), den sog. Stellenwert. So hat die Ziffer 3 in den Zahlen 3, 134, 4357 zwar den gleichen Zahlenwert aber unterschiedlichen Stellenwert. Nicht besetzte Stellen werden mit einer Null gekennzeichnet. Das Stellenwertprinzip ermöglicht es, auf die Angabe von Bündelungseinheiten zu verzichten (statt 1T8H 7Z5E =1875)
Demokurs: Grundlagen der Mathematik für die Grundschule (Arithmetik und Größenbereiche)
| Website: | WueCampus |
| Kurs: | vhb - Demokurs Lehramt |
| Buch: | Demokurs: Grundlagen der Mathematik für die Grundschule (Arithmetik und Größenbereiche) |
| Gedruckt von: | Gast |
| Datum: | Donnerstag, 9. Mai 2024, 03:21 |
Beschreibung
Demokurs
Grundlagen der Mathematik für die Grundschule


Grundlagen der Mathematik für die Grundschule
(Arithmetik − Geometrie − Sachbezogene Mathematik)
(Arithmetik − Geometrie − Sachbezogene Mathematik)

Im Kapitel Stellenwertsysteme finden Sie:
- Allgemeine Informationen über Stellenwertsysteme insbesondere über das dezimale Stellenwertsystem.
- Eigenschaften des Römischen Zahlsystems und Unterschiede zu Stellenwertsystemen.
- Hinweise zum schriftlichen Rechnen in verschiedenen Stellenwertsystemen und zur Umwandlung von Zahldarstellungen.
- Examensaufgabe zum Thema Stellenwertsystem.
- Einsendeaufgaben zum Thema Stellenwertsystem.

Bedeutung für die Grundschule
Dieser Bereich soll Ihnen einen vertieften Einblick in die Aufbauprinzipien des dezimalen Stellenwertsystems vermitteln. Ein fundiertes Hintergrundwissen erleichtert es Ihnen, Schülern und Schülerinnen die grundlegenden Aufbauprinzipien zu erläutern und differenzierte Übungen und Anschauungsmaterialien zur Verfügung zu stellen. So kann z.B. das Bündeln in unterschiedlichen Stellenwertsystemen das Verständnis für den dekadischen Aufbau verdeutlichen.
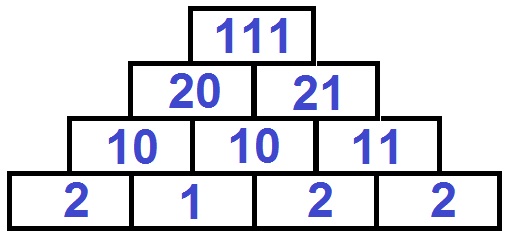
Das Rechnen in nicht-dezimalen Stellenwertsystemen ist zwar kein verpflichtender Bestandteil des bayerischen Lehrplans (vgl. ISB/LEHRPLAN), dieser Themenbereich kann aber dazu beitragen, dass Regeln und Aufbauprinzipien des Stellenwertsystems bewusst werden. Ferner erhält man als Studierende die Möglichkeit Schwierigkeiten selbst zu erleben, die Schüler häufig mit dem Verständnis des Dezimalsystems haben. "Solche Selbsterfahrungen gilt es stets im Hinblick auf unterrichtliche Konsequenzen zu reflektieren." (KRAUTHAUSEN/ SCHERER, 2003, S.21). Sie werden erfahren, wie hilfreich eine Selbstkontrolle oder ein schneller Zugriff auf "1⋅1"- oder "1+1"-Aufgaben ist. Erstellen Sie eigenständig Zahlentürme oder Zahlenmauern in eher ungewohnten Stellenwertsystemen und Sie werden erkennen, welche Schwierigkeiten Ihnen Zahlzerlegungen oder Additionen bereiten können.
Dieser Bereich soll Ihnen einen vertieften Einblick in die Aufbauprinzipien des dezimalen Stellenwertsystems vermitteln. Ein fundiertes Hintergrundwissen erleichtert es Ihnen, Schülern und Schülerinnen die grundlegenden Aufbauprinzipien zu erläutern und differenzierte Übungen und Anschauungsmaterialien zur Verfügung zu stellen. So kann z.B. das Bündeln in unterschiedlichen Stellenwertsystemen das Verständnis für den dekadischen Aufbau verdeutlichen.
Das Rechnen in nicht-dezimalen Stellenwertsystemen ist zwar kein verpflichtender Bestandteil des bayerischen Lehrplans (vgl. ISB/LEHRPLAN), dieser Themenbereich kann aber dazu beitragen, dass Regeln und Aufbauprinzipien des Stellenwertsystems bewusst werden. Ferner erhält man als Studierende die Möglichkeit Schwierigkeiten selbst zu erleben, die Schüler häufig mit dem Verständnis des Dezimalsystems haben. "Solche Selbsterfahrungen gilt es stets im Hinblick auf unterrichtliche Konsequenzen zu reflektieren." (KRAUTHAUSEN/ SCHERER, 2003, S.21). Sie werden erfahren, wie hilfreich eine Selbstkontrolle oder ein schneller Zugriff auf "1⋅1"- oder "1+1"-Aufgaben ist. Erstellen Sie eigenständig Zahlentürme oder Zahlenmauern in eher ungewohnten Stellenwertsystemen und Sie werden erkennen, welche Schwierigkeiten Ihnen Zahlzerlegungen oder Additionen bereiten können.



Dezimalsystem
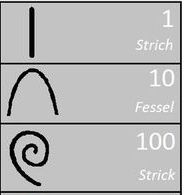
Das dezimale Stellenwertsystem ist das Ergebnis einer jahrtausendelangen Entwicklung. Verschiedene Zahlsysteme unterscheiden sich durch die verwendeten Ziffern und die Art der Bündelung. So nutzten die Ägypter die Hieroglyphenschrift (z.B. entspricht die Lotuspflanze der Zahl 1000) und die Römer verschiedene Zeichen (z.B. X=10) für die Darstellung der Zahlen. Fibonacci (ca. 1170 - 1240) brachte das Rechnen im Zehnersystem aus dem arabischen Raum nach Europa (vgl. SCHEID/ SCHWARZ, 2008, S.47). Andere Zahlsysteme sind das Binärsystem (2er-System) oder das Hexadezimalsystem (16er- System). Stellenwertsystemen (z.B. dekadisches Stellenwertsystem) liegen zwei Prinzipien zugrunde (vgl. KRAUTHAUSEN/ SCHERER, 2003, S.15f.):
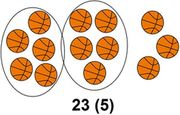
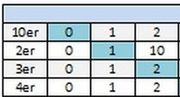
Bündeln im Stellenwertsystem zur Basis 5
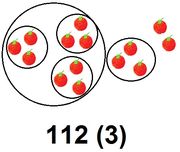
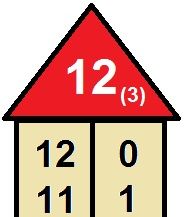
Bündeln im Stellenwertsystem zur Basis 3
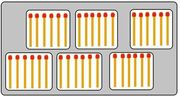
Stellenwertprinzip
Jede Zahl n lässt sich zu jeder Basis b eindeutig folgendermaßen darstellen (b-adische Zahldarstellung).
Sei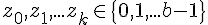 mit
mit 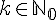 und
und 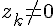 , dann ist
, dann ist
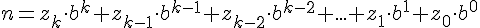
Sei
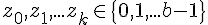 mit
mit 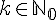 und
und 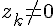 , dann ist
, dann ist 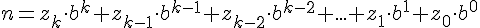
Beispiel:
b-adische Zahldarstellung der Zahl 104 bzgl. der gewählten Basis 6: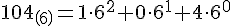 (gesprochen: eins-null-vier bzgl. der Basis 6).
(gesprochen: eins-null-vier bzgl. der Basis 6).
Hinweis: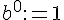
b-adische Zahldarstellung der Zahl 104 bzgl. der gewählten Basis 6:
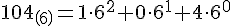 (gesprochen: eins-null-vier bzgl. der Basis 6).
(gesprochen: eins-null-vier bzgl. der Basis 6).Hinweis:
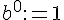
Ist die gewählte Basis b kleiner als 10 (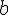 ), dann genügen die uns bekannten Ziffern
), dann genügen die uns bekannten Ziffern 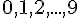 . Ist
. Ist 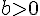 , dann muss man neue ‘Ziffern’ bzw. Symbole einführen. nimmt man beispielsweise im 16er-System, welches häufig in der Informatik verwendet wird, die Buchstaben A, B, C, D, E und F für die 10, 11, 12, 13, 14 und 15 her.
, dann muss man neue ‘Ziffern’ bzw. Symbole einführen. nimmt man beispielsweise im 16er-System, welches häufig in der Informatik verwendet wird, die Buchstaben A, B, C, D, E und F für die 10, 11, 12, 13, 14 und 15 her.
Die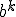 in der b-adischen Zahldarstellung nennt man auch Stufenzahlen.
in der b-adischen Zahldarstellung nennt man auch Stufenzahlen.
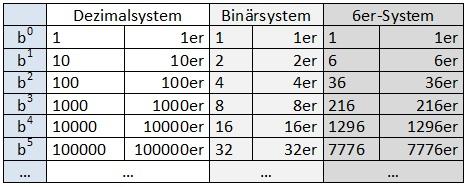
Das dekadische Stellenwertsystem bzw. das Dezimalsystem verwendet eine Zehnerbündelung, entspricht also einem Stellenwertsystem zur Basis 10. Dabei werden 10 Ziffern zur Darstellung benötigt (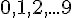 ), wobei unbesetzte Stellen durch eine Null kenntlich gemacht werden.
), wobei unbesetzte Stellen durch eine Null kenntlich gemacht werden.
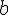 ), dann genügen die uns bekannten Ziffern
), dann genügen die uns bekannten Ziffern 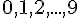 . Ist
. Ist 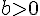 , dann muss man neue ‘Ziffern’ bzw. Symbole einführen. nimmt man beispielsweise im 16er-System, welches häufig in der Informatik verwendet wird, die Buchstaben A, B, C, D, E und F für die 10, 11, 12, 13, 14 und 15 her.
, dann muss man neue ‘Ziffern’ bzw. Symbole einführen. nimmt man beispielsweise im 16er-System, welches häufig in der Informatik verwendet wird, die Buchstaben A, B, C, D, E und F für die 10, 11, 12, 13, 14 und 15 her.Die
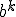 in der b-adischen Zahldarstellung nennt man auch Stufenzahlen.
in der b-adischen Zahldarstellung nennt man auch Stufenzahlen.
Das dekadische Stellenwertsystem bzw. das Dezimalsystem verwendet eine Zehnerbündelung, entspricht also einem Stellenwertsystem zur Basis 10. Dabei werden 10 Ziffern zur Darstellung benötigt (
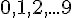 ), wobei unbesetzte Stellen durch eine Null kenntlich gemacht werden.
), wobei unbesetzte Stellen durch eine Null kenntlich gemacht werden. Dass wir heute das dezimale Stellenwertsystem (häufig unbewusst) benutzen, hat historische Gründe und ist sicherlich darauf zurückzuführen, dass die Menschen 10 Finger besitzen. Allerdings wäre auch ein Zwölfersystem denkbar, da erstens Zeiteinheiten in Vielfachen von 12 angeben werden und zweitens die 12 viele Teiler besitzt (vgl. APPELL/ APPELL, 2005, S.107f.).
Historisch gesehen haben schon die Ägypter Zahlen aufbauend auf der 10 dargestellt. Durch Aneinanderreihen von Hieroglyphen konnten natürliche Zahlen geschrieben werden. In Babylonien hatte man dagegen bereits ein 60er-Stellenwerstsystem, welches sich noch heute in der Einteilung der Zeit und der Winkel wiederfindet (vgl. SCHEID/ SCHWARZ, 2008, S.47f.).
Während des Dreißigjährigen Krieges wollten beispielsweise die Schweden anstelle des Dezimalsystems das Zwölfersystem einführen (vgl. APPELL/ APPELL, 2005, S.107f.).
Historisch gesehen haben schon die Ägypter Zahlen aufbauend auf der 10 dargestellt. Durch Aneinanderreihen von Hieroglyphen konnten natürliche Zahlen geschrieben werden. In Babylonien hatte man dagegen bereits ein 60er-Stellenwerstsystem, welches sich noch heute in der Einteilung der Zeit und der Winkel wiederfindet (vgl. SCHEID/ SCHWARZ, 2008, S.47f.).
Während des Dreißigjährigen Krieges wollten beispielsweise die Schweden anstelle des Dezimalsystems das Zwölfersystem einführen (vgl. APPELL/ APPELL, 2005, S.107f.).

Kurz nachgedacht:
- Wahr oder falsch?
(Siehe Interaktion auf der rechten Seite) - Nennen Sie 5 wesentliche Eigenschaften eines Stellenwertsystems!
Lösungshinweis - Vierstellige Zahlen der Form abba (mit
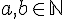 ) heißen ANNA- bzw. OTTO-Zahlen.
) heißen ANNA- bzw. OTTO-Zahlen.
- Bilden Sie zu einer ANNA-Zahl die "andere" ANNA-Zahl mit gleichen Ziffern und subtrahieren Sie die kleinere von der größeren. Rechnen sie mehrere dieser Aufgaben und vergleichen Sie Ihre Ergebnisse. Was fällt Ihnen auf?
Lösungshinweis - Begründen Sie ihre Entdeckung beispielgebunden an einer Stellenwerttafel, indem Sie die kleinere Zahl mit Plättchen legen und durch Verschieben der Plättchen die größere ANNA- Zahl entstehen lassen.
Lösungshinweis
- Bilden Sie zu einer ANNA-Zahl die "andere" ANNA-Zahl mit gleichen Ziffern und subtrahieren Sie die kleinere von der größeren. Rechnen sie mehrere dieser Aufgaben und vergleichen Sie Ihre Ergebnisse. Was fällt Ihnen auf?



Examensaufgaben
Frühjahr 2010/ Thema Nr. 2
- Erläutern Sie die Begriffe Stellenwertsystem und Dezimalsystem!
- Beschreiben Sie, wie man mithilfe von Materialien Verständnis für die Darstellung von Zahlen im Dezimalsystem entwickeln kann!
- Entwerfen Sie eine Unterrichtseinheit zum Thema „Verstehen von dreistelligen Zahlen“!
Frühjahr 2009/ Thema Nr. 1
-
- Erläutern Sie die Darstellung natürlicher Zahlen in einem Stellenwertsystem.
- Berechnen Sie im Vierersystem: 101(4) – 33(4) und 112300(4) : 130(4)
- Diskutieren Sie die Bedeutung des Bündelns und Entbündelns für den Mathematikunterricht in der Grundschule.
- Entwerfen Sie eine Unterrichtseinheit zur Einführung der schriftlichen Addition mit Übertrag.
Herbst 2003/ Thema Nr. 2 1
- Erläutern Sie für natürliche Zahlen folgende Begriffe: Bündeln, Stellenwert, Stellenwertsystem!
- Beschreiben Sie verschiedene Bündelmaterialien und diskutieren Sie deren Einsatz im Mathematikunterrich der Grundschule (Jahrgangsstufe 1-4)!
- Entwerfen Sie eine Unterrichtseinheit für die Einführung des Rundens von natürlichen Zahlen!
Herbst 2002/ Thema Nr. 2
-
- Erläutern Sie die Darstellung natürlicher Zahlen in einem Stellenwertsystem.
- Berechnen Sie mithilfe von Normalverfahren im Dreiersystem: 1013-223 und 1203·2103.
- Diskutieren Sie die Bedeutung nicht- dekadischer Stellenwertsysteme in der Grundschule.
- Entwerfen Sie eine Unterrichtseinheit zur Einführung der schriftlichen Addition mit Übertrag.
Frühjahr 1999/ Thema Nr. 3
-
- Erläutern Sie die Darstellung natürlicher Zahlen in einem Stellenwertsystem!
- Vergleichen Sie die römische Zahldarstellung mit der Darstellung im dezimalen Stellenwertsystem!
- Erläutern Sie unterrichtliche Aktivitäten zur Erarbeitung des dekadischen Stellenwertsystems!
- Arbeiten Sie eine Unterrichtseinheit für die 4.Jahrgangsstufe aus, in der Vorstellungen zur Zahl 1 Million aufgebaut werden.



Grundlagen der Mathematik für die Grundschule
(Arithmetik – Geometrie – Sachbezogene Mathematik)
(Arithmetik – Geometrie – Sachbezogene Mathematik)

Im Kapitel Größenbereiche finden Sie:
- Begriffsbestimmung und Definition.
- Rechnen, Messen, Schätzen und Überschlagen mit und von Größen.
- Examensaufgaben zum Thema Größenbereiche.
- Einsendeaufgaben zum Thema Größenbereiche.

Bedeutung für die Grundschule
In der sachbezogenen Mathematik nimmt der Größenbereich eine wesentliche Rolle ein. Mit Sachaufgaben wird versucht Alltagsbezüge herzustellen und daher ist es nicht verwunderlich, dass die meisten von ihnen mit Größen zu tun haben. Das Verständnis der Größenbereiche ist im Modellierungsprozess eine wichtige Voraussetzung zur Lösung von Sachaufgaben.
Sachaufgaben werden ab der 1. Jahrgangsstufe durchgehend bis zur 4. Jahrgangsstufe behandelt. Die verwendeten Maßzahlen und Maßeinheiten orientieren sich dabei an den Zahlenraumerweiterungen in der Arithmetik. Dieser Themenbereich soll Ihnen nun das theoretische Hintergrundwissen von Größenbereichen vermitteln, damit Sie Begriffe wie Größen, Größenbereich, Repräsentant usw. unterscheiden, erläutern und korrekt verwenden können. "Auch wenn Größen zu unserem alltäglichen Leben gehören, sind sie nicht weniger abstrakt als Zahlen" (vgl SCHIPPER, 2009, S. 230). Definitionen und Beispiele zeichen Ihnen, warum es möglich ist Größen zu vergleichen und mit ihnen zu rechnen.
Darüber hinaus werden Sie die Unterschiede von Messen, Schätzen, Überschlagen und Runden kennenlernen, damit Sie erstens die Begriffe korrekt verwenden und zweitens Aufgaben zu allen Varianten der Arbeit mit Größen anbieten. Diesbezüglich werden auch die Begriffe Repräsentant und Stützpunktwissen näher erläutert.

Stellenwertsysteme
- Dezimalsystem
- Römisches Zahlsystem
- Rechnen in unterschiedlichen Stellenwertsystemen
- Umwandlung von Zahldarstellungen
- Examensaufgaben
- Grundrechenarten
- Rechengesetze
- Examensaufgaben
Teilbarkeit
- Eigenschaften
- Endstellenregel
- Quersummenregel
- Examensaufgaben
Größenbereiche
- Begriffsbestimmung und Definition
- Rechnen, Messen und Schätzen
- Examensaufgaben